This post describes my submission to the Minecraft Open-endedness challenge 2021. The submission was evaluated with the video below and the code here. This post will detail the methods and tools used for the submission and give hints for future work.
If you want a quick description of the work, have a look at the video:
Introduction
Motivation
My current research deals with evolution in complex systems and specifically cellular automata (CA). I want to see if we can use such systems to construct open-ended evolving simulations that create an endless stream of ever more complex structures and patterns.
Minecraft being a grid world, it has a similar structure to some common flavors of CA. I was excited to see if I could port some of these ideas from the world of CA to Minecraft, where a player can interact with the structures in real time and change their evolution.
The ideal goal would be to create a CA that behaves in an open-ended way. Such CA would create new and progressively more complex structures autonomously. By mapping the states of such CA to block types in Minecraft, we could watch these structures emerge in-game. A feedback loop could be naturally added where a user’s actions are mapped back to the CA, enabling a form of “controlled” evolution.
Neural cellular automata
Such CA doesn’t exist yet, and our main hope for the time being is to approach this behavior on a reduced domain. Neural cellular automata, introduced in [1], can be trained with gradient descent to grow a fixed pattern stable under small perturbations from a small fixed seed.
Example patterns learned by NCA, created with Mordvintsev et al's colab notebook
In each of the examples above, a separate CA was trained on a pattern starting from a single black pixel. We extend this by training a single NCA on multiple patterns from different seeds. Instead of a single black cell, a small number of cells are arranged into simple shapes.
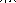
Example seed patterns
NCA have a lot of parameters (low compared to a regular neural network but still high compared to the information that is encoded in the system). This allowed us to learn more than one pattern (or larger patterns) without adding parameters in the architecture. The resulting patterns are of slightly lower quality but still stable under perturbations and able to grow.
A NCA trained on 4 animal patterns with different seeds
We turned this idea into a “game” by allowing user interaction with the evolving CA through Minecraft. Our system is not open-ended by itself, but needs human interaction to play with the shapes and seed patterns. This is in the spirit of open-ended games like Picbreeder [2] where players choose which generated patterns to mutate or evolve from. The algorithms can generate endless novelty but our human eyes provide the missing step to make it open-ended.
Players can manipulate seeds in the game to create progressively more complex creatures out of the ones learned by the NCA.
Hybrids created on a single NCA by recombining parts of the initial seeds
Evaluation
We try to address the evaluation criteria from the competition’s website:
Submission will be evaluated by a panel of independent researchers based on -but not restricted to- the following criteria:
Divergence: Open-ended algorithms are not expected to slow down or converge but rather keep expanding and generating more complex outputs over time.
Diversity: Does the algorithm produce entities with strong phenotypic diversity? […]
Complexity: Can the algorithm produce complex entities or entities interactions that give rise to complex systems? Are hierarchical and modular structures present?
Ecological interactions: Do the created entities interact with each other? […]
Life-Like properties: Inspiration may be taken from other attributes of living systems […]
- Divergence: seeds can be combined as long as one wants. By splitting the seeds and using arbitrarily large canvasses, the possibilities are infinite.
- Diversity: The diversity is based on the diversity of patterns the NCA was trained on originally. From this, the algorithm produces combinations of the original patterns.
- Complexity: The produced hybrids are arguably modular and hierarchical.
- Ecological interactions: Different pieces of the evolved seeds may interact with each other, giving rise to surprising and unexpected structures, but this is arguably not what the organizers meant with this item. There are no proper ecological interactions in our system
- Life-like properties: Mutations and crossovers that we observe can be related to some living systems.
Methods
Modular seeds
The patterns learned by NCA may have different spatial symmetries and structures. By using seed patterns that take advantage of these structures we can help making the hybrids modular.

Seed displayed on top of the target pattern. One part of the seed should code for the body and the other for the head
In the example above, the NCA learns to grow the pattern from this “double” seed: a head-seed and a body-seed. Because the fully trained NCA know how to repair a damaged pattern, it can actually grow the full pattern from each of these two sub-seeds. When two or more patterns are learned, we can swap sub-seeds to create hybrids.

Hybrid giraffe-gorilla obtained by using the head-seed of a giraffe and the body-seed of a gorilla
Genome seeds
We also try another way of encoding information about the patterns in a compact and modular form: genome seeds.

Genome seeds: unique patterns of cells
Future work
Seed engineering
Compression in NCA
NCA trained on multiple patterns implement some form of data compression. Information about each pixel of the target images as well as instructions to grow the pattern from any position is encoded in the NCA parameters in some form. A natural follow-up question would be to look at the storage capacity of these NCA and if their low number of parameters could make it an interesting robust and error-correcting compression device.
 Open-endedness
Open-endedness