Kullback-leibler divergence

tags

Applied maths

Definition

The KL divergence is not symmetric. For \(P, Q\) defined on the same probability space \(\mathcal{X}\), KL of \(Q\) from \(P\) is \[ KL(P, Q) = \sum_{x \in \mathcal{X}} P(x) \log\left( \frac{P(x)}{Q(x)} \right) \]

It has two main interpretations:

• It is the information gain from using the right probability distribution \(P\) instead of \(Q\) or the amount of information lost by approximating \(P\) with \(Q\).
• The average difference in code length for a sequence following \(P\) and using a code optimized for \(Q\) to encode it.

Forward and reverse KL

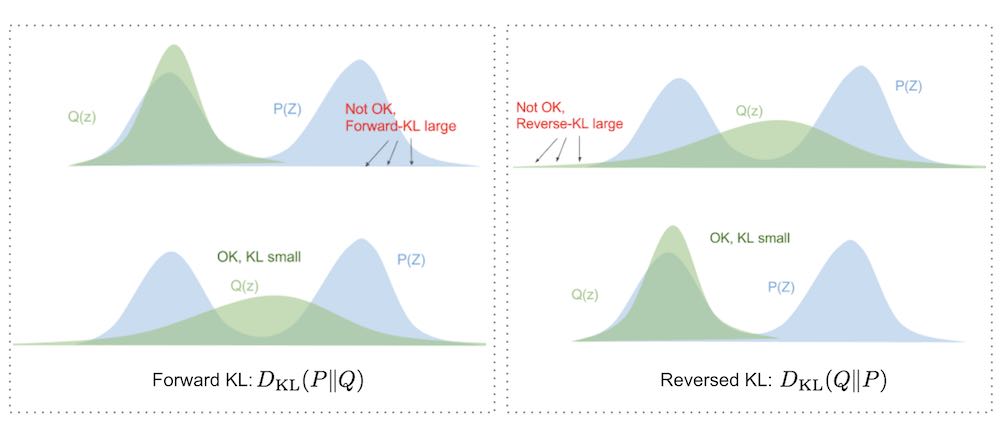
Eric Jang’s blog has an interesting visual explanation of the difference between forward and backward KL.

So in summary, minimizing forward-KL “stretches” your variational distribution \(Q(Z)\) to cover over the entire \(P(Z)\) like a tarp, while minimizing reverse-KL “squeezes” the \(Q(Z)\) under \(P(Z)\).