Stochastic optimization for large scale optimal transport

A university project about Stochastic Optimal Transport.

Description

The goal of this project was to reproduce and extend results from [1] which uses the Stochastic Average Gradient algorithm (SAG [2]) to solve regularized optimal transport problems faster. We compare SAG with other optimization algorithms, including SAGA [3]. After comparing the regularized optimal transport convergence results for these algorithms, I studied an optimal school placement and allocation problem in several French regions.

The figures below show some results of solving the semi-discrete optimal transport problem between the school positions and the population density. This enables finding an assignment mapping areas to school which is optimal with respect to a metric on the studied space. The metric here is absolute distance, but it should rather be the real travel distance to be realistic.

School positions in the Rennes school administrative area. The image shows the Bretagne region of France with the borders of the city districts as well as red crosses for marking the schools.

The repartition of schools in the Rennes school administrative area (source: data.gouv.fr).

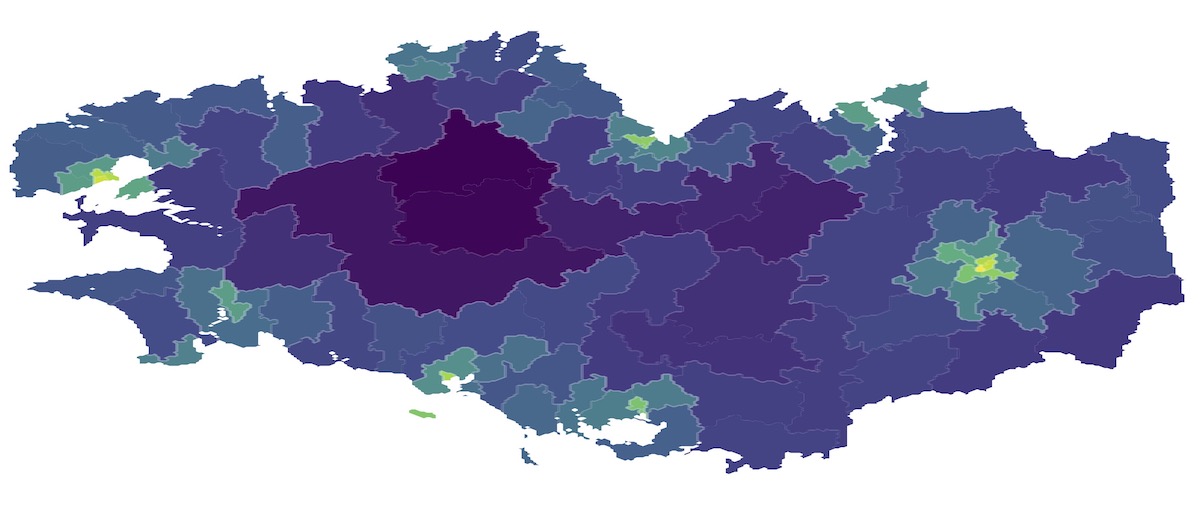
Excavation animation

Relative population density in each communal district of the Bretagne region (log-scale, source: data.gouv.fr).

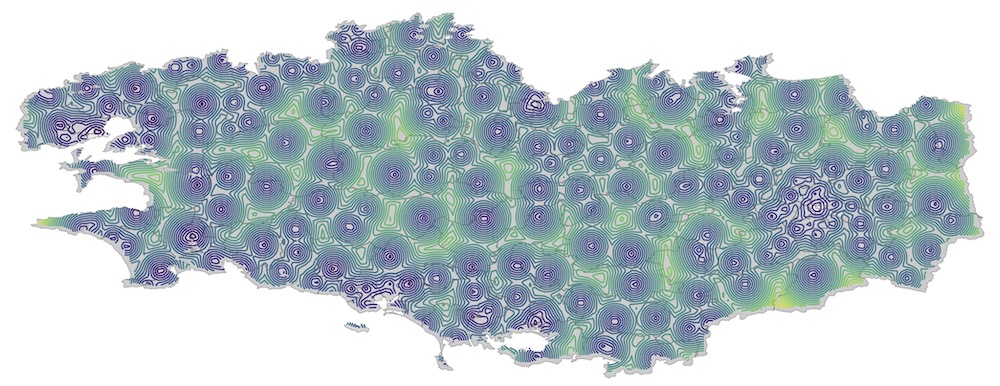
Excavation animation

Results of the semi-discrete optimal transport estimation between the population density (continuous) and the school locations (discrete). The image shows the $\bar{c}$-transform, see the report for details. An optimal assignment can be extracted from this distribution.

This project was my final evaluation for the course Mathematical Foundations Of Data Science taught by Gabriel Peyré in 2019.

References

  1. Genevay, A., Cuturi, M., Peyré, G. & Bach, F..Stochastic Optimization for Large-scale Optimal Transport. in Advances in Neural Information Processing Systems 29 (eds. Lee, D. D., Sugiyama, M., Luxburg, U. V., Guyon, I. & Garnett, R.) 3440–3448 (2016).
  2. Schmidt, M., Roux, N. L. & Bach, F..Minimizing Finite Sums with the Stochastic Average Gradient. arXiv:1309.2388 [cs, math, stat] (2013).
  3. Defazio, A., Bach, F. & Lacoste-Julien, S..SAGA: A Fast Incremental Gradient Method With Support for Non-Strongly Convex Composite Objectives. arXiv:1407.0202 [cs, math, stat] (2014).
Last modified 2019.01.07