Double descent

tags
Neural network training, Neural networks
resources
(Belkin et al. 2019)

Double descent is a phenomenon usually observed in neural networks, where the usual bias-variance tradeoff seems to break down: test error keeps decreasing as we over-parametrize the network or add more training examples. This was observed for over-parametrized neural networks in (Geman et al. 1992).

An illustration from (caption is also adapted from the paper) (Belkin et al. 2019):

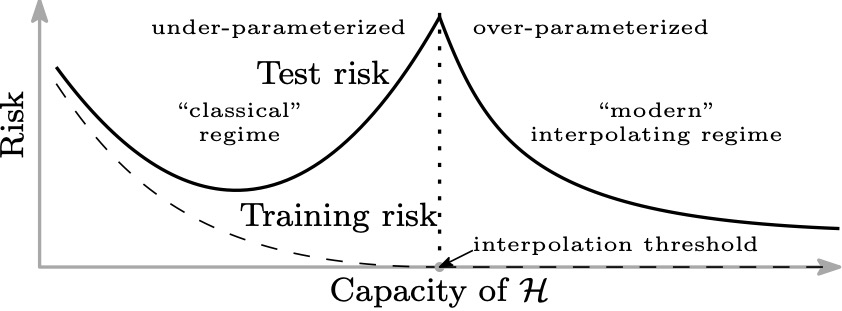
This shows training and test risk curves as a function of the capacity. The curve follows the usual bias-variance tradeoff but then starts going down again.

Figure 1: Illustration of the double descent effect in deep neural networks. The double descent risk curve, which incorporates the U-shaped risk curve (i.e., the “classical” regime) together with the observed behavior from using high capacity function classes (i.e., the “modern” interpolating regime), separated by the interpolation threshold. The predictors to the right of the interpolation threshold have zero training risk.

Bibliography

  1. . . "Reconciling Modern Machine Learning Practice and the Bias-variance Trade-off". Arxiv:1812.11118 [cs, Stat]. http://arxiv.org/abs/1812.11118.
  2. . . "Neural Networks and the Bias/variance Dilemma". Neural Comput. 4 (1):1–58. DOI.

Links to this note

Last changed | authored by

Comments


← Back to Notes