- source
- (Adams et al. 2017)
- tags
- Open-ended Evolution, Cellular automata
Summary
This paper defines two properties for dynamical systems which are claimed to be related to open-ended evolution: Unbounded evolution (UE) and Innovation (INN). The combination of these two properties makes a system open-ended according to this paper’s definition For such properties to be possible, a system has to be decomposed into two entities that interact with each other:
- an organism,
- an environment.
For the purpose of measuring “open-endedness”, the environment is ignored and the author wish to see if the organism can do more than what it could do if it was an isolated system.
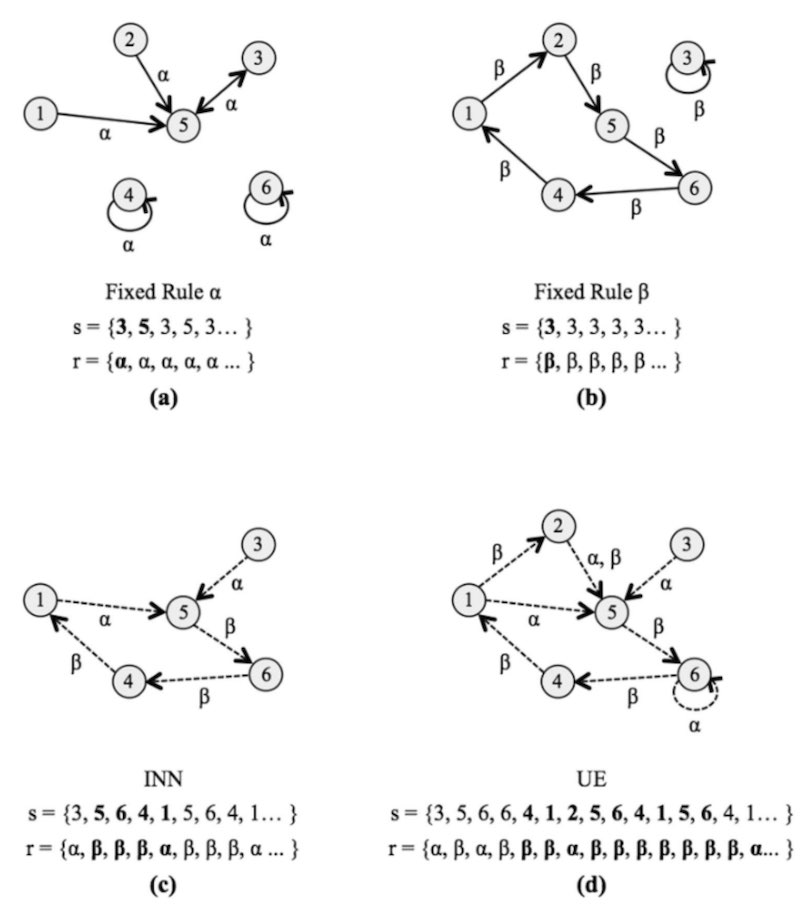
Figure 1: Figure 1 from the paper. Different systems might exhibit INN or UE. To go past its intrinsic Poincare recurrence time, a system needs to interact with an environment.
Unbounded evolution
A system decomposed into an organism \(o\) and an environment \(e\) is said to exhibit UE if there exist a (state or rule) trajectory longer than the Poincaré recurrence time of the equivalent isolated organism.
Innovation
To exhibit innovation, a system \(o + e\) must have a trajectory not contained within the possible trajectories of an isolated version of \(o\).
Experiments with CA extensions
The authors experiment with a few extensions of the cellular automaton model to incorporate these organism/environment dynamics.
Bibliography
- Alyssa Adams, Hector Zenil, Paul C. W. Davies, Sara Imari Walker. . "Formal definitions of unbounded evolution and innovation reveal universal mechanisms for open-ended evolution in dynamical systems". Scientific reports 7 (1):997. DOI.