Cellular automata

tags
Emergence, Chaos, Artificial Intelligence
resources
Wikipedia, (Von Neumann, Burks 1966; Wolfram 2002)

Definition

A cellular automaton is a computational model defined with respect to a regular grid of individual elements (called cells). Each of those cells can be in one of a finite number of states — alive or dead, \(\{1, 2, 3\}\), etc.

A cellular automaton’s evolution is simulated in discrete timesteps. At each new timestep, cells are updated according to a local evolution rule. The rule is a table or function mapping every possible state of a cell and their local neighborhoods to a new state. It follows that a CA is a kind of dynamical system.

There are multiple ways to define the topology of the grid, rules, local neighborhoods and simulation steps. Some well known types of automata are listed below

Elementary cellular automata

Cellular automata on 1D grids, with two states and neighborhood radius 1 (middle cell + one cell on each side) are called Elementary cellular automata — or ECA.

Reversible cellular automata

Reversible cellular automata are CA rules with one and only one image and pre-image. Each step of the evolution is reversible.

Cyclic cellular automata

Cellular automata rules

The rules of a cellular automaton can be created in different ways.

Rule table representation

One useful representation is a large lookup table that maps any possible configuration of the neighborhood of a cell to a new value for that cell. This is suitable only for small neighborhood sizes and number of states since the lookup table can get extremely large.

In this representation, creating or sampling a rule may be seen as choosing a value for each of the entries of the lookup table.

Uniform sampling

If we independently sample each of the entries for the table with uniform probability the resulting rule are “average”, and tend to be behaving in a very chaotic manner.

Dirichlet-based sampling

Another approach is to deliberately bias the sampling towards a particular state. This way most transitions lead to a single state, leading to more “stable” CA with a background state.

This sampling is done as follows:

  • For \(k\) states, sample from a $k$-dimensional Dirichlet distribution with \((\alpha_1, \cdots, \alpha_k) = (\alpha, \cdots, \alpha)\) with \(\alpha\) a constant value \(< 1\) (to ensure bias towards a single state).
  • This yields a vector \((\lambda_1, \cdots, \lambda_k)\) that sums to 1 which will be the proportions of each state in the table. Because of the Dirichlet distribution one \(\lambda\) is likely to be much bigger than the others.
  • Sample the transitions in the rule table according to these proportions.

Cellular automata and Reaction-diffusion systems

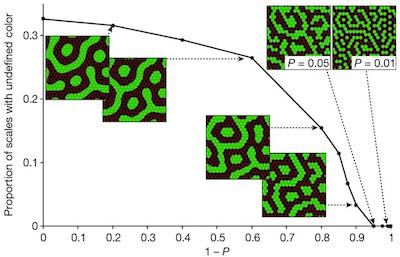
I just realized that cellular automata and reaction-diffusion systems are strongly related. This might be a well known fact but it seemed particularly striking when looking at the following image from (Manukyan et al. 2017) it seems clear that there is a continuum between the two models. Also this illustrates the applicability of cellular automata to models of biological life.

A example of similarities between CA and reaction-diffusion

Cellular automata in Image processing

Papers about using cellular automata in image processing (Selvapeter, Wim Hordijk 2009; Wongthanavasu, Ponkaew 2013)

Some cellular automata have a characteristic “blob-preserving” behavior where parts of the space get organized in large blobs. This behavior is very similar to an application of local median. See this twitter link for an animated example.

Coarse-graining CA

I am very attracted to this idea of coarse graining CAs. This is reminiscent of physical systems where the inner working of a system are mostly opaque to an observer and we only see a complex macro-behavior. In the case of CAs this might be the key to overcoming this problem of seemingly impossible increase of complexity beyond a certain point if we keep looking at individual cells. This also allows an external observer to understand a complex behavior happening in billions of cells visually. It can be done with Autoencoders.

CA as regular languages

CAs can be studied with regular languages.

Evolution and CAs

Why would things evolve in a CA? I was running interesting CAs for several 100s of thousands of steps recently and realized that I did not really know what I would be expecting to happen in one of those without any input from outside. Could it be that, by just pure luck, some things start to evolve in it? That some species or life-like forms emerge?

If this is even possible, what are the odds of this happening? Was it how it worked in our case (earth)? Did just random particle interactions in a large soup gave rise to a complete miracle? So far from my experiment I have seen complex previously unseen structures emerge during an automaton evolution, but this has never gone farther than just a few big structures appearing and not staying this way. I believe it is a bias to think that those structures would have been suited to keep evolving because their brittleness did not let them survive. Therefore the (unpractical) way forward might be to let those things run and see what happens, where the “surviving” would be the ones left after all this.

I’m wondering whether some kind of external input to those small “universe” could help give rise to more complex behavior. Because I am starting to think that even with the most efficient system possible, the probability of seeing a complex structure appearing decreases somewhat exponentially with the complexity of the structure (or according to a power law).

Obviously I have no idea about all this and this is just based on speculation. But I’ve yet to see reasonable evidence that we can run a CA for a large number of time steps without any kind of input and see this increase in complexity happen by itself. Maybe the key would be to help it? But is it even possible?

Playing god with cellular automata

I believe an exciting part of working on spontaneous emergence, artificial evolution, and cellular automata is the fact that it really feels like playing with a microverse. Some relevant recent pop-cultures examples involving this idea include:

Each one of those cellular automata can be seen as a universe, with its own laws of physics (update rule) and initial big bang-like configuration (the initial state). Most combinations of the laws of physics are not stable and create completely disordered systems, but some rare configurations give rise to large structures sifting through space and exhibit highly non-trivial macro behavior (2-3 cells wide up to several 100s of cells-wide). Many of these structures interact in different ways, some create siblings and children structures while other get destroyed very quickly.

This transition from randomness to order could be seen in the case of our universe as the 4 physical forces pulling together particles into bigger and bigger structures which form a large system with a lot of emptiness and some localized structures. In this analogy, our planet and even our galaxy are just a microscopic ripple on of those giant structures, but what if we could make this kind of ripple happen in a much smaller universe, with much simpler laws? This is more or less what we are trying to achieve with cellular automata.

Obviously starting from scratch is hard, and it might not be necessary to let this microverse evolve in a closed way without interacting with it somehow.

This point of view is related to The Simulated reality hypothesis and Zuse’s thesis, and is an interesting argument for the universe being a computer simulation — and even a CA.

Cellular automata and philosophy

See Stanford Encyclopedia of Philosophy’s entry for cellular automata

Cellular automata models of Physics

Gerard ’t Hooft has studied the possibility of formulating quantum mechanics as a cellular automaton (Hooft 2014).

Bibliography

  1. . . "Theory of Self-reproducing Automata". IEEE Transactions on Neural Networks 5 (1):3–14. https://cba.mit.edu/events/03.11.ASE/docs/VonNeumann.pdf.
  2. . . A New Kind of Science. Champaign, IL: Wolfram Media. https://www.wolframscience.com/nks/.
  3. . . "A Living Mesoscopic Cellular Automaton Made of Skin Scales". Nature 544 (7649):173–79. DOI.
  4. . . "Cellular Automata for Image Noise Filtering". In 2009 World Congress on Nature & Biologically Inspired Computing (nabic), 193–97. Coimbatore, India: IEEE. DOI.
  5. . . "Cellular Automata for Pattern Recognition". In Emerging Applications of Cellular Automata, edited by Alejandro Salcido. InTech. DOI.
  6. . . "The Cellular Automaton Interpretation of Quantum Mechanics". Arxiv:1405.1548 [quant-ph]. http://arxiv.org/abs/1405.1548.

Links to this note

Last changed | authored by

Comments


← Back to Notes