- tags
- Unconventional computing, Cellular automata
- resources
- (Mitchell 2005; Wolfram 2002)
Cellular automata are computational models capable of interesting emergent behavior. A major challenge is to understand which CA rules are doing useful or efficient computations. It is not clear how these systems could be programmed or made to compute a particular function.
Hand-engineered CA rules
Below images show CA rules that can compute non trivial functions (Images are from (Wolfram 2002), see A new kind of science online ). These examples are nice but likely challenging to produce for complex computations.
Binary adder CA rule 
Square CA rule 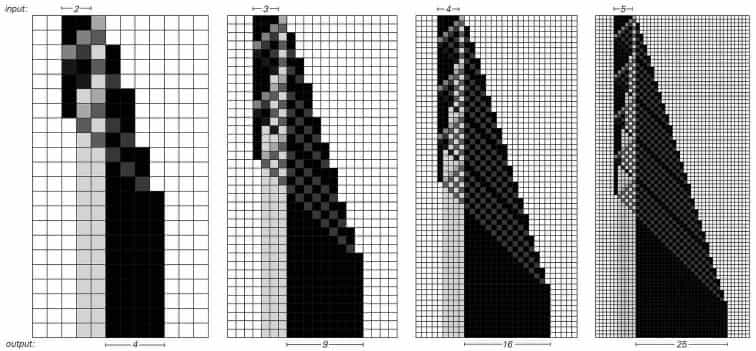
Prime CA rule (sieve of Eratosthenes) 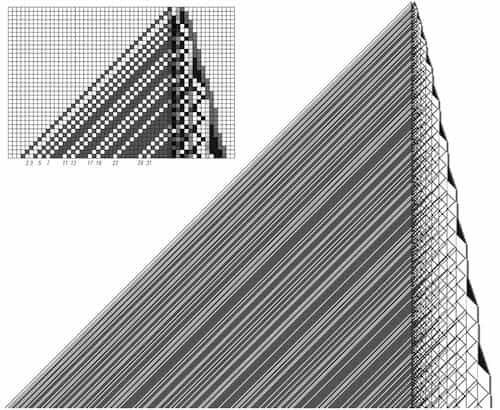
Hyperbolic space
A cellular automaton can solve the 3-SAT problem in polynomial time on a pentagrid — grids of pentagons — in hyperbolic space (Margenstern 1999).
Evolution of CA rules
CA rules can also be evolved with Genetic algorithms to perform a particular type of computation. Because it uses a genetic algorithm, this method requires a clear reward/objective function to be effective, which might not be achievable for complex functions were input/output pairs aren’t enough of a signal for finding a solution. (Packard 1988; Mitchell et al. 1997)
Link with reservoir computing
Computation in cellular automata are difficult to construct and control finely, which is why many have tried to use the reservoir computing with cellular automata framework to try and discover useful computations in cellular automata.
Bibliography
- Melanie Mitchell. . "Computation in Cellular Automata: A Selected Review". In Non-standard Computation, 95–140. Weinheim, FRG: Wiley-VCH Verlag GmbH & Co. KGaA. DOI.
- Stephen Wolfram. . A New Kind of Science. Champaign, IL: Wolfram Media. https://www.wolframscience.com/nks/.
- Maurice Margenstern. . "A Polynomial Solution for 3-SAT in the Space of Cellular Automata in the Hyperbolic Plane.". J. UCS 5 (9):563–73. DOI.
- Norman H. Packard. . "Adaptation Toward the Edge of Chaos". Dynamic Patterns in Complex Systems 212. World Scientific:293–301.
- Melanie Mitchell, James P Crutchfield, Rajarshi Das. . "Evolving Cellular Automata to Perform Computations". In Handbook of Evolutionary Computation, edited by Thomas B�ck, David B Fogel, and Zbigniew Michalewicz. IOP Publishing Ltd. DOI.